慣性モーメント

円板

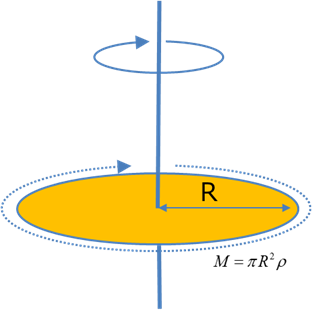
・水平に回る場合（レコードのように）

半径，R，で重心位置を中心に回転する場合を考えます．

ここでは，厚みを考えませんので，質量M，の場合，面密度ρとの関係は，

\( \Large \displaystyle M = \pi R^2 \ \rho \)

となります．

半径ｒからr+dr，の間のリングの面積は，

\( \Large \displaystyle S = \pi (r+dr)^2 - \pi r^2 = \pi (r^2 + 2r \cdot dr + dr^2 - r^2) = \pi (2r \cdot dr + dr^2) \simeq 2 \pi r \cdot dr \)

となりますので，半径０からRまでのリング部分を積分すればいいことになります．慣性モーメントは，

\( \Large \displaystyle J_{disk-01} = \int_{0}^R r^2 \cdot \rho \cdot 2 \pi r \ dr = 2 \pi \rho \left[ \frac{r^4}{4} \right]_{0}^R = 2 \pi \rho \frac{1}{4} R^4
= \frac{M}{\pi R^2} \cdot 2 \pi \frac{1}{4} R^4 = \boldsymbol{\frac{1}{2} MR^2 }\)

となります．

・縦の場合（団扇を回す？ように）

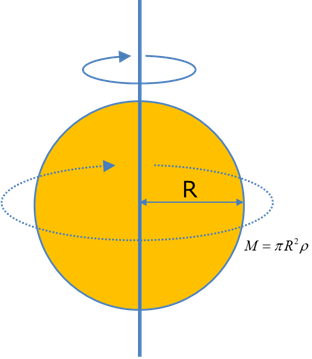
団扇を回す？ように回した場合を考えていきます．

この場合には，中心からの距離は使いにくいので，図のように，線の慣性モーメントを求め，積分します．

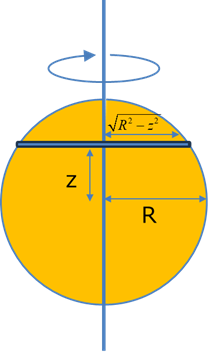
円の中心からｚだけ離れた線分の慣性モーメントを考えます．

\( \Large \displaystyle J_{line} = \int_{- \sqrt{R^2 - z^2} }^{\sqrt{R^2 - z^2} } x^2 \cdot \rho \ dx = \rho \left[ \frac{x^3}{3} \right]_{- \sqrt{R^2 - z^2} }^{\sqrt{R^2 - z^2} } = \frac{2 \rho}{3} (R^2 - z^2)^{3/2} \)

れは円板の中の一部の線の慣性モーメントなので，z方向にーRからRまで積分すればいいので，

\( \Large \displaystyle J_{line} = \int_{- R }^{R } \frac{2 \rho}{3} (R^2 - z^2)^{3/2} dz = 2 \int_{0 }^{R } \frac{2 \rho}{3} (R^2 - z^2)^{3/2} dz\)

を計算すればいいことになります．変数変換して，

\( \Large \displaystyle z = R \ sin \theta \)

\( \Large \displaystyle dz = R \ cos \theta \ d \theta \)

\( \Large \displaystyle 0 \sim z \sim R \)

\( \Large \displaystyle 0 \sim \theta \sim \frac{ \pi}{2} \)

\( \Large \displaystyle J_{disk-02} = 2 \int_{0 }^{R } \frac{2 \rho}{3} (R^2 - z^2)^{3/2} dz
= \frac{4 \rho}{3} \int_{0 }^{\frac{ \pi}{2} } (R^2 - R^2 \ sin^2 \theta )^{3/2} R \ cos \theta d \theta \)

\( \Large \displaystyle = \frac{4 \rho}{3} \int_{0 }^{\frac{ \pi}{2} } (R^2 \ cos^2 \theta )^{3/2} R \ cos \theta d \theta \)

\( \Large \displaystyle = \frac{4 \rho \ R^4}{3} \int_{0 }^{\frac{ \pi}{2} } cos^4 \theta \ d \theta \)

この積分は，ここ，にあるような公式を使って，

\( \Large \displaystyle \int_{0 }^{\frac{ \pi}{2} } cos^4 \theta \ d \theta =
\int_{0 }^{\frac{ \pi}{2} } \frac{ 3 + 4 \ cos \ 2 \theta + cos \ 4 \theta}{8} d \theta \)

第二項，第三項は，θがπ，2πとなり，cos関数は０となります．したがって，

\( \Large \displaystyle \int_{0 }^{\frac{ \pi}{2} } cos^4 \theta \ d \theta =
\int_{0 }^{\frac{ \pi}{2} } \frac{ 3 }{8} d \theta
= \frac{ 3 }{8} \displaystyle \left[ \theta \right]_0^{\frac{ \pi}{2}}
= \frac{ 3 \pi}{16}\)

\( \Large \displaystyle J_{disk-02} = \frac{4 \rho \ R^4}{3} \int_{0 }^{\frac{ \pi}{2} } cos^4 \theta \ d \theta
= \frac{4 \rho \ R^4}{3} \frac{ 3 \pi}{16} =\frac{ \pi \rho \ R^4}{4} \)

ここでは，厚みを考えませんので，質量M，の場合，面密度ρとの関係は，

\( \Large \displaystyle M = \pi R^2 \ \rho \)

となります．したがって，

\( \Large \displaystyle J_{disk-02} = \frac{ \pi \ R^4}{4} \frac{M}{\pi R^2} = \boldsymbol{\frac{1}{4} MR^2 }\)

となります．このように水平に回すより慣性モーメントが半分になっています．ついつい空気抵抗が大きそうと考えちゃいますが，ここでは慣性モーメントを考えていますので，空気抵抗は関係ありませんね．

円柱

円柱も円板と同様の考え方ですが，積分の取り方，質量と密度との関係が変わってきます（３次元になったので）

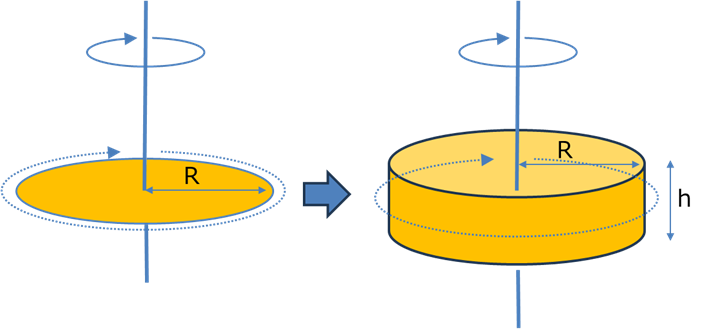
円周方面の積分の後，高さ方向の積分を行います．

\( \Large \displaystyle J_{cylinder} = \int_0^h dx \int_{0 }^{R } 2 \pi r \ dr \)

ここでは，厚みを考えるので，質量M，の場合，体積密度ρとの関係は，

\( \Large \displaystyle M = \pi R^2 \ h \ \rho \)

となります．

最初の積分は，

\( \Large \displaystyle J_{disk-01} = \int_{0 }^{R } 2 \pi r \ dr = 2 \pi \rho \left[ \frac{r^4}{4} \right]_0^R =2 \pi \rho \frac{R^4}{4}\)

これを高さ方向に積分するので，

\( \Large \displaystyle J_{cylinder} = \int_0^h 2 \pi \rho \frac{R^4}{4} dx = 2 \pi \rho \frac{R^4}{4} \left[ x \right]_0^h = 2 \pi \rho \frac{R^4}{4} h \)

密度を代入すると，

\( \Large \displaystyle J_{cylinder} = 2 \pi \frac{R^4}{4} \frac{M}{ \pi R^2 h} = \boldsymbol{\frac{1}{2} M R^2} \)

となり，円板の場合と同じ計算式となります．Mの定義が異なることに注意です．

次ページは，球の慣性モーメント，を検討していきます．